Response and FIR filter removal

Usage Questions
1

Hi

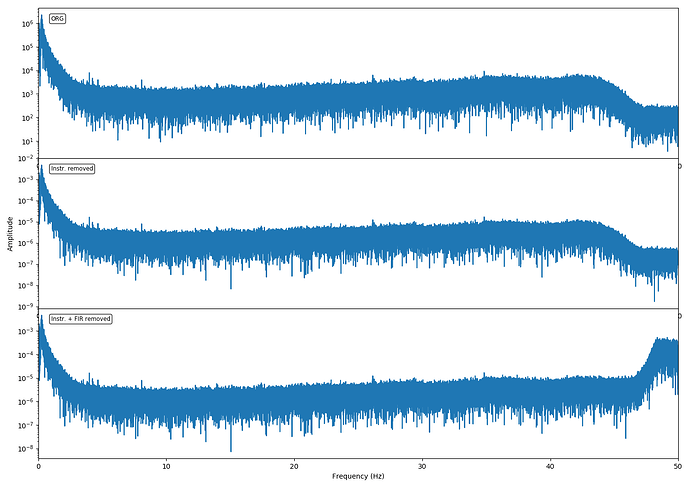
Historically we have not included FIR filter coefficients and decimation stages in our metadata. Discovering however that most(?) other networks do we have started a process towards doing so. However, it seems that this triggers some un-expected behaviour when approaching the Nyquist frequency upon instrument removal. Now while the FIR filter removal should affect the spectral amplitudes close to Nyquist I’m are a bit surprised about the quite high spectral amplitudes resulting from the process (see figure comparing instrument removal including FIR filters or not) thus wondering if this is reasonable or if I’m missing out on something.

FIR
FIR1400×988 90 KB

To remove the instrument response I’m using the remove_response() method on the Stream object (code example below) and set argument end_stage in the case I wish not to remove the FIR filters.

I’m also wondering a bit about in which order FIR filters and are removed. E.g. when invoking the remove_response() method will it remove the stages in the order they are listed in the metadata (i.e. sensor first, then digitizer, then FIR filters from first to last) or in reverse order (i.e. last FIR filter first and sensor last)? Does it matter which order the stages are removed?

I guess when removing the FIR filters it only makes sense to remove the last FIR filter as previous FIR filter were applied at higher sampling rates and should have minimal to no impact at frequencies up to the Nyquist frequency following the last decimation step, right? However in the response files typically the FIR filters are listed in the order they were applied which means that the last FIR filter is listed last. Upon removal of instrument responses using the remove_response() method one can specify the first and last stage to include but as there may be several FIR filters in the meta data then removing the last FIR filter means that also the previous ones will be removed unless remove response if invoked twice (one time removing the last FIR filter and one time removing the sensor and digitizer response). Now while removing the earlier FIR filters should not affect the data as argued above it does add quite some time to the duration of the operation so when processing a lot of data this can become impractical. Would it perhaps be reasonable to add an argument to the remove_response() method, say use_stage, which takes an iterable where the stages to be removed can be listed (thereby allowing to skip all FIR filters except the last)?

import matplotlib.pyplot as plt
import numpy as np

# Load data and meta data
inv = read_inventory("UP.BLMU.HHZ.dataless")
tr0 = read('UP.BLMU..HHZ.D.20230808T0100-T0130.mseed')[0]

# Demean data and remove linear trend
tr0 = tr0.detrend(type='linear')
tr0 = tr0.detrend(type='demean')
tr0.taper(type='hann',max_percentage=0.005,max_length=2)

# Remove instrument responses only
tr1 = tr0.copy()
tr1.remove_response(inventory=inv, pre_filt=[0.002, 0.008, 49.9, 49.99], end_stage=4)

# Remove instrument responses and FIR filters
tr2 = tr0.copy()
tr2.remove_response(inventory=inv, pre_filt=[0.002, 0.008, 49.9, 49.99])

# Prepare plot
fig = plt.figure(figsize=(14, 10))
axs = []
axs.append(fig.add_subplot(3,1,1,sharex=None))
axs.append(fig.add_subplot(3,1,2,sharex=axs[0]))
axs.append(fig.add_subplot(3,1,3,sharex=axs[1]))

# Make sure data vector to fft is of length equal to 2**n (to speed thing up)
# and set up a frequency vector
n_data = len(tr0.data)
n_use = 2
while n_use*2 <= n_data:
   n_use *= 2
fs = [k*tr0.stats.sampling_rate/n_use for k in range(n_use//2+1)]

# Compute and plot spectral amplitudes
fft0 = np.fft.rfft(tr0.data, n=n_use)
amp0 = np.abs(fft0)
axs[0].semilogy(fs,amp0)
fft1 = np.fft.rfft(tr1.data, n=n_use)
amp1 = np.abs(fft1)
axs[1].semilogy(fs,amp1)
fft2 = np.fft.rfft(tr2.data, n=n_use)
amp2 = np.abs(fft2)
axs[2].semilogy(fs,amp2)

# Add some labels and trim axes
tag = ['ORG', 'Instr. removed', 'Instr. + FIR removed']
for i in range(3):
   axs[i].set_xlim([0, 50])
   axs[i].text(0.02,0.95, tag[i], transform=axs[i].transAxes, fontsize="small", ha='left', va='top', bbox=dict(boxstyle="round", fc="w", alpha=0.8))
axs[1].set_ylabel("Amplitude")
axs[2].set_xlabel("Frequency (Hz)")
fig.tight_layout()
fig.subplots_adjust(hspace=0)

plt.show(block=True)

UP.BLMU…HHZ.D.20230808T0100-T0130.mseed (218.5 KB)
UP.BLMU.HHZ.dataless (24 KB)

The instrument at the site is a nanometrics with a centaur digitizer. The attached dataless file were downloaded directly from the digitizer.

2

Response removal is (mostly) a single step in the frequency domain. In any case the complete response is removed in a single multiplication step onto the data spectrum. You can have a look at the plot=True option in remove_response() (see docs).

Currently that’s not easily possible as we use evalresp under the hood and that only has options for start and end stage.

3

Ok, so I guess in order to understand why I get such an amplification of the amplitudes towards the Nyquist frequency I need to take a closer look at the FIR filter in the frequency domain, right? From you experience, is the amplifications seen in the figure above reasonable (guess water leveling is dampening them of as when a colleague did the exercise in sac there was an even greater amplification/peak towards Nyquist) or is this more likely an artefact (naively it seems to be affecting quite a large part of the spectra starting already around 42 Hz for my 100 Hz which seems a lot to me, but then again I’m quite in-experienced here so ergo calling out to your experience)?

I’m a bit curios though here as removal of only sensor and digitizer response goes in a flash but also removing the FIR filter increase the time by several seconds for each FIR filter removed. Why is it so slow to compute the frequency response of the FIR filters (which I guess is the added operation that needs to be done compared to just removing the sensor and digitizer response - well there are some additional flops involved but those should also go in an instance)?

So I guess the the work-around would be to call remove_response() twice, one time removing just sensor and digitizer response and one time removing just the last FIR filter, right?

4

I mean, I guess it’s a similar issue as with the long period end of the instrument response. If the response has the anti aliasing filters properly in it and you simply multiply with the inverse instrument response, you just blow up parts of the spectrum that don’t really have a lot of energy in it. Of course if you leave out the anti aliasing filter stages during response removal, then basically your instrument response goes flat all the way to Nyquist and in consequence the inverse instrument response that is multiplied onto your data spectrum will also be flat, so no blowing up of that part of the data spectrum.

If I understand correctly your data is recorded at 100 Hz, so looking at your spectra up top, everything seems quite OK to me, just pre filter out a bit further away from Nyquist. I’d just ignore everything above 45 Hz, really, unless you are specifically looking at something at very high frequencies (I’m assuming you don’t). But then, I’d just use higher sampling rates to begin with, to be honest. To me it looks like that’s where the anti aliasing filters really start to kick in massively, from looking at the data spectrum. Maybe something like pre_filt=[..., ..., 40, 45]?

Well, I don’t know the details of the computation inside evalresp, but intuitively, I’d also expect a computation from a handful poles/zeros to be faster than if having to work on several hundreds to thousands of coefficients in the FIR filters.

Personally, I usually just remove the full response and make sure the pre filter settings are fine. But it really depends on your needs, I guess. Seems like you’re doing something absolutely time critical in realtime? Otherwise I can’t imagine this operation being the bottleneck in any larger workflow.

5

Well, for now this is just a matter of academic interest rather than a real world need. I’m only aware of a single case where a colleague actually had a good reason to look at our data close to Nyquist (hard to go back in time to adjust the recording to a higher sampling rate).

Nah, just not really a bottleneck nor a larger workflow, just me having an impatient personality that get itches when things go from 1s run time to 50s runtime, coupled to a need to understand the cause. You’ve helped a little bit along the way here but I guess I finally have to suck it up and learn some signal processing to calm the itch